Математика против идеализма

С недавнего времени, когда я ловлю себя на мысли что что-то сделал не «идеально», и что можно было достичь лучшего результата поработав над мелочами достаточно усрердно — я вспоминаю вот эти картинки.

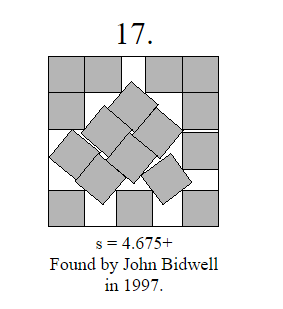
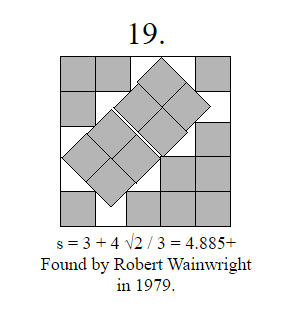
Это иллюстрации математически доказанных принципов самого эффективного размещения квадратов со стороной n, в квадрате со стороной s.

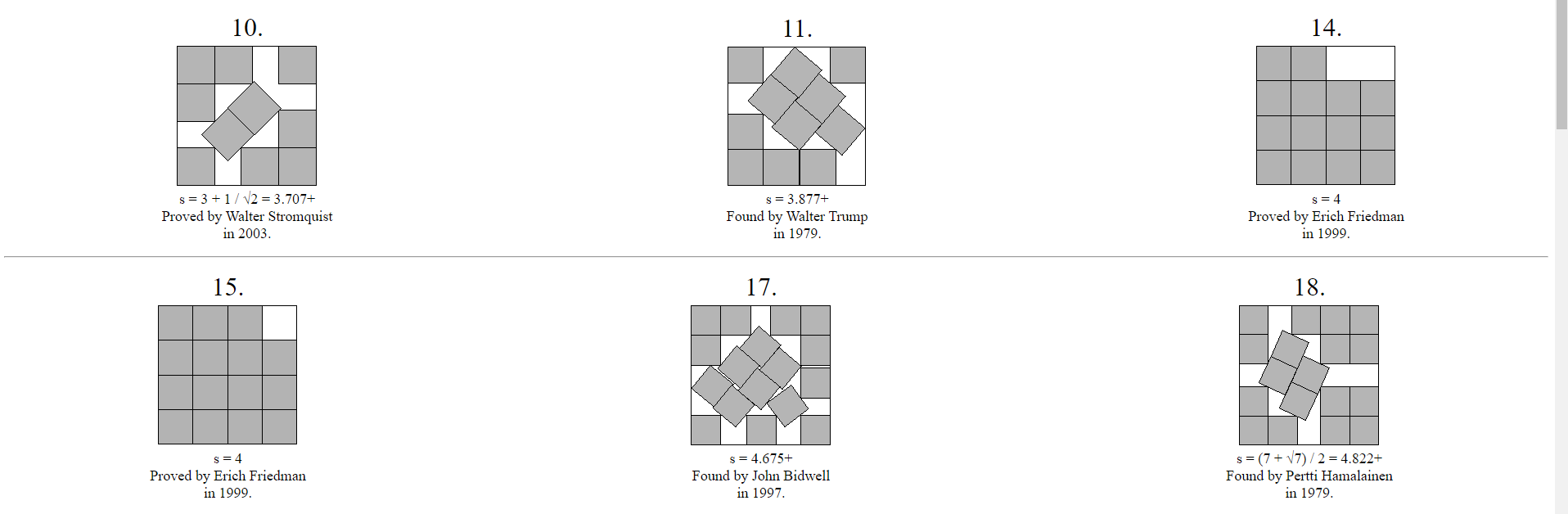
Больше примеров можно посмотреть вот тут. И да, с чётным количеством квадратов там всё выглядит как из рая перфекциониста (ожидаемо), а вот паттерны умещения нечётного количества квадратов выглядят вот так. Как ад перфекциониста, но, рай математика.

Идея этих задач проста: вам нужно уместить выбранное количество квадратов с одинаковой длинной стороны так, чтобы сторона квадрат, в который они будут вписаны получилась как можно меньше. Если получится сделать это так, что квадрат в который они вписаны получится меньше — значит и занимаемая ими площадь будет меньше. А значит — и метод эффективней.

Вот картинка, наглядно это иллюстрирующая: 17 квадратов вписаны «красиво» и «правильно». Квадрат в который они вписаны, во втором случае — чу-у-уть меньше первого, а значит — эффективней.

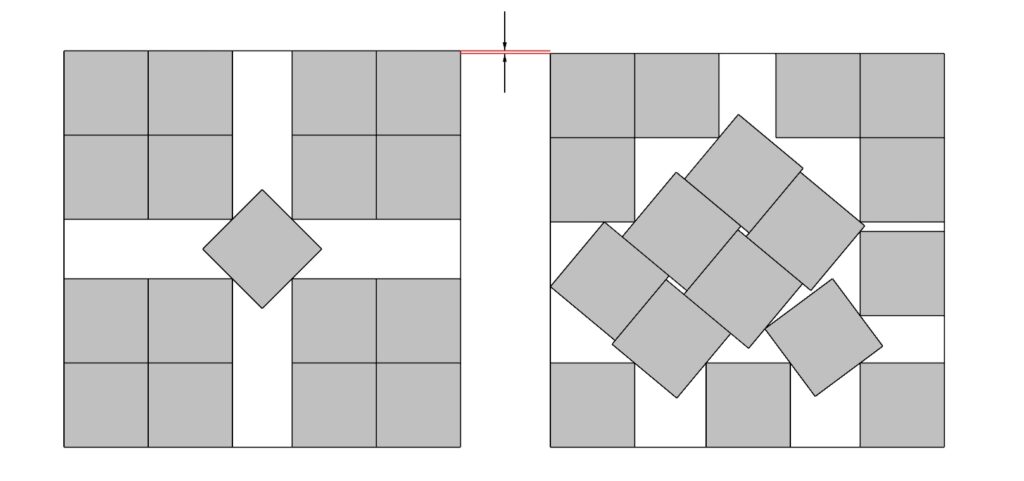
Что нам даёт этот пример? Очередное напоминание: эффективность — это далеко не всегда изящество и красота. По крайней мере, с внешней точки зрения. И, чтобы понять истинный замысел иногда — нужно внимательней вмотреться в суть вещи.

Такие дела.